Error correcting codes

This article is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below and there is another article based on the talk here.

We are surrounded by information and are constantly receiving and transmitting it to other people all over the world. With good reason we can call the 21st century the information age. But whenever a message is being sent, be it over the phone, via the internet, or via satellites that orbit the Earth, there is the danger for errors to creep in. Background noise, technical faults, even cosmic rays can corrupt the message and important information may be lost. Rather amazingly, however, there are ways of encoding a message that allow errors to be detected, and even corrected, automatically. Here is how these codes work.

The 15th century scribe, manuscript illuminator, translator and author Jean Miélot at his desk.

Error detecting codes

The need for the detection of errors has been recognised since the earliest scribes copied manuscripts by hand. It was important to copy these without error, but to check every word would have been too large a task. Instead various checks were used. For example, when copying the Torah the letters, words, and paragraphs were counted, and then checked against the middle paragraph, word and letter of the original document. If they didn't match, there was a problem.

Modern digital information is encoded as sequences of 0s and 1s. When transmitting binary information a simple check that is often used involves a so-called hash function, which adds a fixed-length tag to a message. The tag allows the receiver to verify the delivered message by re-computing it and comparing it with the one provided in the message.

A simple example of such a tag comes from including a check or parity digit in each block of data. The simplest example of this method is to add up the digits that make up a message and then append a 1 if the sum is odd and a 0 if it is even. So if the original message is 111 then message sent is 1111, and if the original message is 101, then the message sent is 1010. The effect of this is that every message sent should have digits adding up to an even number. On receiving the transmission the receiving computer will add up the digits, and if the sum is not even then it will record an error.

An example of the use of this technology can be found on the bar codes that are used on nearly all mass-produced consumer goods sold. Such consumer products typically use either UPC-A or EAN-13 codes. UPC-A describes a 12-digit sequence, which is broken into four groups. The first digit of the bar code carries some general information about the item: it can either indicate the nationality of the manufacturer, or describe one of a few other categories, such as the ISBN (book identifier) numbers. The next five digits are a manufacturer's identification. The five digits that follow are a product identification number, assigned by the manufacturer. The last digit is a check digit, allowing a scanner to validate whether the barcode has been read correctly.

Similar check digits are used in the numbers on your credit card, which are usually a sequence of decimal digits. In this case the Luhn algorithm is used (find out more here).

Error correcting codes

Suppose that we have detected an error in a message we have deceived. How can we proceed to find the correct information contained in the message? There are various approaches to this. One is simply to (effectively) panic: to shut the whole system down and not to proceed until the problem has been fixed. The infamous blue screen of death, pictured below and familiar to many computer operators, is an example of this.

Blue Screen of Death on Windows 8.

The rationale behind this approach is that in some (indeed many) cases it is better to do nothing than to do something which you know is wrong. However, all we can do at this point is to start again from scratch, and we lose all information in the process.

A second approach called the automatic repeat request (ARQ), often used on the Internet, is for the message to be repeated if it is thought to contain an error. We do this all the time. For example if you scan in an item at the supermarket and the scanner does not recognise it, then you simply scan it in again.

However, this option is not available to us if we are receiving information from, say, a satellite, a mobile phone or from a CD. In this case if we know that an error has been made in transmission then we have to attempt to correct it. The general idea for achieving correction is to add some extra data to a message, which allows us to recover it even after an error has been made. To do this, the transmitter sends the original data, and attaches a fixed number of check bits using an error correcting code (ECC). The idea behind this is to make the symbols from the different characters in the code as different from each other as possible, so that even if one symbol in the code was corrupted by noise it could still be distinguished from other symbols in the code. Error correcting codes were invented in 1947, at Bell Labs, by the American mathematician Richard Hamming.

Illustration of the U.S./European Ocean Surface Topography Mission (OSTM)/Jason-2 satellite in orbit. Image: NASA-JPL/Caltech

To understand how error correcting codes work we must define the Hamming distance between two binary strings. Suppose that we have two six-bit strings such as 1 1 1 0 1 0 and 1 0 1 1 1 1. Then the Hamming distance is the number of digits which are different. So in this case the Hamming distance is 3. If one bit in a symbol is changed then it has a Hamming distance of one from its original. This change might be due to the action of noise, which has corrupted the message. If two strings are separated by a large Hamming distance, say 3, then they can still be distinguished even if one bit is changed by noise. The idea of the simplest error correcting codes is to exploit this fact by adding extra digits to a binary symbol, so that the symbols are a large Hamming distance apart.

I will illustrate this with a simple example. The numbers from 0 up to 7, written in binary, are:

000 (0) 001 (1) 010 (2) 011 (3)
100 (4) 101 (5) 110 (6) 111 (7)

(You can read more about binary numbers here, or simply believe me.)

Many of these strings are only one Hamming distance apart. For example a small amount of noise could turn the string for 2 into the string for 3. We now add some extra parity digits (we explain the maths behind these later) to these codes to give the code

000 000 (0) 001 110 (1) 010 011 (2) 011 101 (3)
100 101 (4) 101 011 (5) 110 110 (6) 111 000 (7)

The point of doing this is that each of these codes is a Hamming distance of 3 apart. Suppose that the noise is fairly low and has the effect changing one bit of a symbol. Suppose we take the symbol 101 011 for 5 and this changes to (say) 100 011. This is a Hamming distance of one from the original symbol and a distance of at least two from all of the others. So if we receive 100 011 what we do is to find the nearest symbol on our list to this. This must be the original symbol, and we correct 100 011 to 101 011 to read the symbol without error.

Space flight, Facebook and CDs

All error correcting codes use a similar principle to the one above: receive a string, if it's not on the list find the closest string on the list to the one received, correct the string to this one. A lot of mathematical sophistication is used to find codes for more symbols which will work in the presence of higher levels of noise. Basically the challenge is to find symbols which are as different from each other as possible. Alongside the development of a code is that of an efficient decoder, which is used to correct corrupted messages fast and reliably.

In case you don't remember what a CD looks like (or are too young to ever have seen one). Image: Arun Kulshreshtha , CC BY-SA 2.5.

Another example of an error correcting code is the Reed-Solomon code invented in 1960. The first commercial application in mass-produced consumer products appeared in 1982, with the CD, where two Reed–Solomon codes are used on each track to give even greater redundancy. This is very useful when having to reconstruct the music on a scratched CD.

Today, Reed–Solomon codes are widely implemented in digital storage devices and digital communication standards (for example digital TV), although they are now being replaced by low-density parity-check (LDPC) codes. Reed–Solomon coding is very widely used in mass storage systems to correct the burst errors associated with media defects. This code can correct up to 2 byte errors per 32-byte block. One significant application of Reed–Solomon coding was to encode the digital pictures sent back by the Voyager space probe, which was launched in 1977 and took the first satellite pictures of Jupiter, Saturn and the far planets.

A major recent user of error correction is on Facebook, which is possibly the largest repository of information in the world. It is estimated that 300 million photos are stored on Facebook every day. This information is stored in vast data banks around the world, mostly on spinning discs. Whilst the individual failure rate of a disc is very low, there are so many discs required to store the information that the chance of one of the discs failing at any one time is high. When this happens the data on the disc is recovered efficiently and quickly by using a Reed-Solomon code, so that Facebook can continue without interruption.

Some mathematics

In this last section we will give some mathematical detail for those who are interested. (If you aren't interested in the details, you can skip to the next article.) It is far from simple to work out codes which are both efficient and robust, and a whole branch of mathematics, coding theory, has been developed to do it.

The Hamming (7,4) code is similar to the Hamming code above, only in this case three parity bits are added to a message with four information bits (rather than a message with three information bits , as above). If $x$ is the string $x = (d_1,d_2,d_3,d_4)$ of the information (which is four bits long), then the transmitted symbol $y$ is seven bits long and is given by $y=(p_1,p_2,d_1,p_3,d_2,d_3,d_4)$ where $p_1$ , $p_2$ and , $p_3$ are the parity bits. These parity bits are added so that groups of the digits in the code have an even number of 1s. The following diagram shows what these groups are: each $p_ i$ is represented by a circle and the group of bits consisting of this $p_ i$ and the $d_ i$ that also lie in this circle must contain an even number of 1s.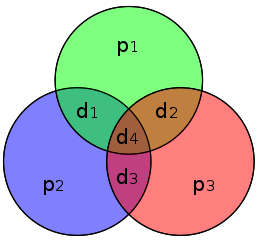

Image: CBurnett, CC BY-SA 3.0.

For example, this means that if $x=(1,1,0,1)$ then because $d_1$ , $d_2$ and $d_4$ lie in the circle of $p_1$ and together contain three 1s, $p_1$ must be equal to 1 to make the number of 1s in the green circle even. The parity bits $p_2$ and $p_3$ must both be equal to 0. Therefore $y=(1, 0, 1, 0, 1, 0, 1).$

Now suppose that $y$ is incorrectly transmitted so that one bit is corrupted and we receive instead the signal $z=(1, 0, 1, 0, 1, 1, 1)$ . Let’s see if we can correct this error. The group of bits that belong to the green circle ( $p_1$ , $d_1$ , $d_2$ and $d_4$ ), have the correct parity (even), and the groups of bits that belong to the blue and red circles each have the wrong parity (odd). Since the only information bit that belongs to both the red and the blue circle is $d_3$ , it’s $d_3$ that must be the offending bit. And that’s correct.

In a more abstract setting

$y = G x,$

where $G$ is a 7x4 code generator matrix and all operations are calculated in modular 2 arithmetic. Since a 7x4 matrix multiplied by a vector of length 4 gives a vector of length 7, the multiplication gives a vector of the correct length, that is, three parity bits are added. This multiplication is a linear transformation, and the Hamming (7,4) code is an example of a linear code. If a corrupted form $z$ of the message $y$ is received, then the bit for which the error is made is found by using a second, and cleverly constructed, parity checking 3x7 matrix $H$ . This matrix is constructed so that if there is no error, then

$d=Hz$

should be the zero vector. If it is not the zero vector, then an error has occurred. The vector $d$ will correspond to one of the columns of $H$ and the location of this column (first, second, third, etc) indicates where in the original string the error was made. Then it is easily possible to construct a 4x7 matrix $R$ to recover the original symbol so that

$x = R z.$

Évariste Galois, drawn from memory by his brother in 1848, sixteen years after his death.

The Reed-Solomon code is more sophisticated in its construction. In the classic implementation of the Reed-Solomon code the original message is mapped to a polynomial with the terms of the message being the coefficients of the polynomial. The transmitted message is then given by evaluating the polynomial at a set of points. As in the Hamming (7,4) code, the Reed-Solomon code is a linear transformation of the original message. Decoding works by finding the best fitting message polynomial. All of the multiplications for the polynomial are performed over mathematical structures called finite fields. The theory behind the construction of these codes uses advanced ideas from the branch of mathematics called Galois theory, which was invented by the French mathematician Évariste Galois when he was only 19, and at least 150 years before it was used in CD players.

About this article

This article is based on a talk in Budd's ongoing Gresham College lecture series. A video of the talk is below and there is another article based on the talk here.

Chris Budd.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.